Pengertian Elips
Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya dari dua titik tertentu (disebut fokus) selalu tetap. Elips merupakan salah satu bentuk irisan kerucut yang terbentuk ketika sebuah bidang memotong kerucut dengan kemiringan yang lebih kecil dari kemiringan garis pelukis kerucut.
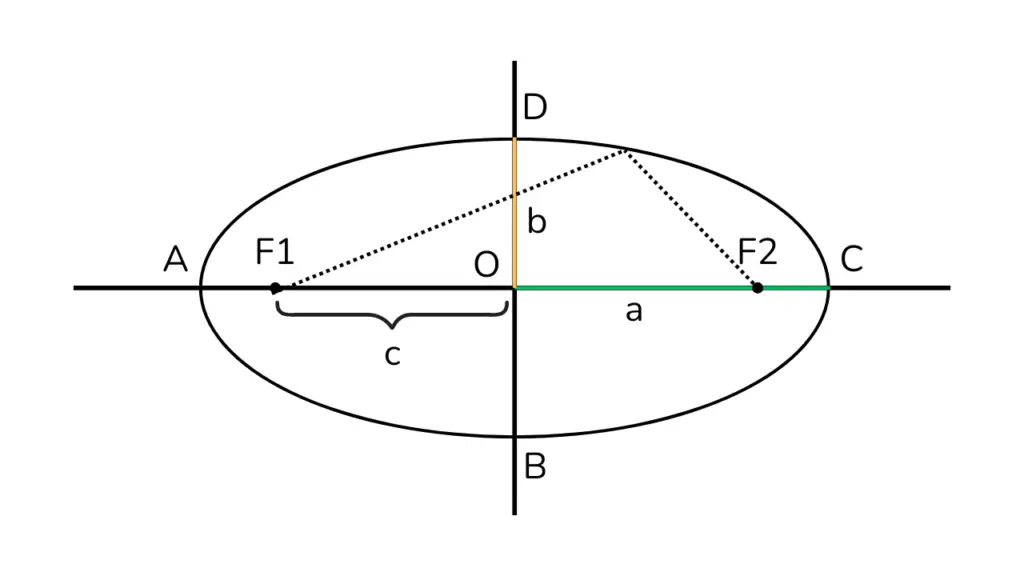
Gambar di atas menunjukkan elips dengan dua fokus F₁ dan F₂. Untuk setiap titik P pada elips, jumlah jarak |PF₁| + |PF₂| selalu konstan.
Persamaan Standar Elips
Persamaan standar elips dengan pusat di titik O(0,0) dan sumbu panjangnya terletak pada sumbu x:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Sedangkan persamaan standar elips dengan pusat di titik O(0,0) dan sumbu panjangnya terletak pada sumbu y:
$$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $$
Dalam kedua persamaan ini, a adalah setengah sumbu panjang (sumbu mayor) dan b adalah setengah sumbu pendek (sumbu minor), dengan a > b > 0.
Unsur-unsur Elips
Beberapa unsur penting dalam elips:
1. Pusat elips: Titik tengah elips, biasanya dilambangkan dengan O.
2. Fokus: Dua titik tetap yang menjadi acuan penentuan elips. Fokus elips dilambangkan dengan F₁ dan F₂.
3. Sumbu mayor: Sumbu terpanjang pada elips, dengan panjang 2a. a sendiri adalah panjang O ke C atau O ke A.
4. Sumbu minor: Sumbu terpendek pada elips, dengan panjang 2b. c sendiri adalah panjang O ke B atau O ke D.
5. Jarak fokus (2c): Jarak antara kedua fokus, dengan c² = a² – b².
6. Titik A, B, C, dan D merupakan titik puncak elips.
7. Eksentrisitas (e): Nilai yang menunjukkan seberapa “bulat” atau “pipih” suatu elips, didefinisikan sebagai e = c/a, dengan 0 < e < 1.
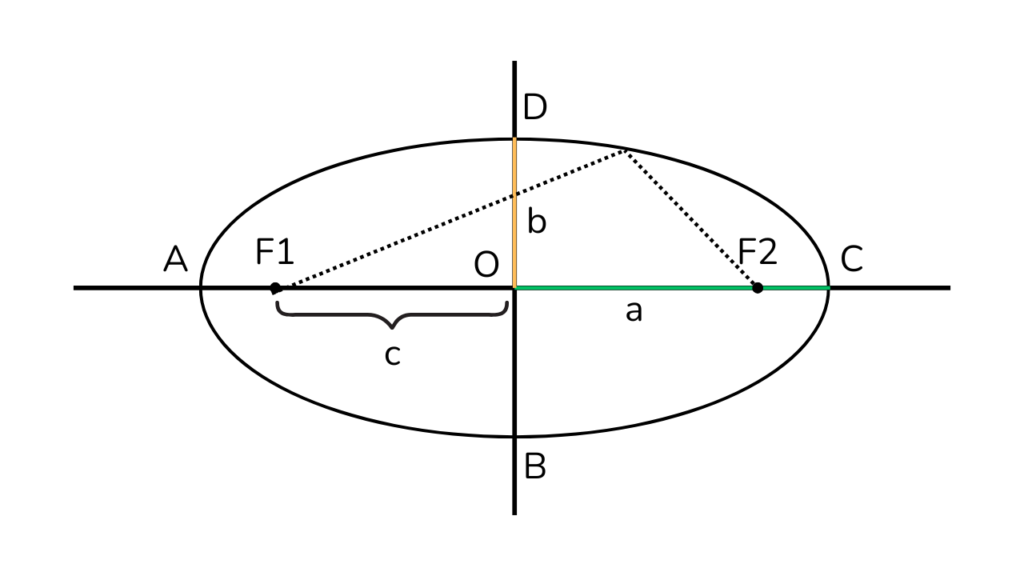
Gambar di atas menunjukkan parameter-parameter utama elips: sumbu mayor (2a), sumbu minor (2b), dan fokus (F₁ dan F₂).
Lokasi Fokus
Jika sumbu mayor terletak pada sumbu x, maka posisi fokus adalah:
F₁(-c, 0) dan F₂(c, 0), dengan c = $ \sqrt{a^2 – b^2} $
Jika sumbu mayor terletak pada sumbu y, maka posisi fokus adalah:
F₁(0, -c) dan F₂(0, c), dengan c = $ \sqrt{a^2 – b^2} $
Persamaan Elips dengan Pusat di P(h, k)
Jika elips berpusat di titik P(h, k), persamaannya menjadi:
Jika sumbu mayor sejajar sumbu x: $$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$
Jika sumbu mayor sejajar sumbu y: $$ \frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1 $$
Aplikasi Elips dalam Kehidupan
Elips memiliki banyak aplikasi dalam kehidupan sehari-hari dan sains:
1. Orbit planet: Planet-planet bergerak dalam lintasan berbentuk elips dengan matahari berada di salah satu fokusnya (Hukum Kepler I).
2. Arsitektur: Ruangan berbentuk elips memiliki sifat bahwa suara yang berasal dari satu fokus akan dipantulkan ke fokus lainnya.
3. Kedokteran: Teknologi pemecah batu ginjal (lithotripsy) memanfaatkan sifat elips untuk memfokuskan gelombang kejut ke batu ginjal.
4. Optik: Cermin elips dapat memantulkan semua sinar yang berasal dari satu fokus ke fokus lainnya.
Sifat Refleksi Elips
Salah satu sifat penting elips adalah sifat refleksinya. Jika sebuah sinar cahaya atau gelombang dipancarkan dari salah satu fokus elips, maka sinar tersebut akan dipantulkan ke fokus lainnya. Sifat ini dimanfaatkan dalam berbagai aplikasi seperti ruang bisik, alat terapi medis, dan desain tertentu pada teleskop.
Menggambar Elips
Elips dapat digambar secara manual dengan metode “tali dan dua paku”. Dengan menancapkan dua paku pada bidang datar (sebagai fokus), kemudian mengikat tali pada kedua paku dengan panjang tali tetap, dan meregangkan tali tersebut dengan pensil, maka jejak pensil tersebut akan membentuk elips.
Contoh Soal Elips
Contoh 1: Menentukan Persamaan Elips
Tentukan persamaan elips yang memiliki fokus di titik (±3, 0) dan panjang sumbu utamanya adalah 10.
Penyelesaian:
Diketahui c = 3 dan 2a = 10, maka a = 5.
Kemudian, b² = a² – c² = 5² – 3² = 25 – 9 = 16, sehingga b = 4.
Karena fokus terletak pada sumbu x, maka persamaan elipsnya adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$
Contoh 2: Menentukan Panjang Sumbu dan Koordinat Fokus
Diketahui persamaan elips $$ \frac{x^2}{36} + \frac{y^2}{20} = 1 $$. Tentukan:
a) Panjang sumbu mayor dan minor
b) Koordinat titik fokus
c) Eksentrisitas elips
Penyelesaian:
Dari persamaan $$ \frac{x^2}{36} + \frac{y^2}{20} = 1 $$, dapat dilihat bahwa a² = 36 dan b² = 20.
a) Panjang sumbu mayor = 2a = 2√36 = 2(6) = 12 satuan
Panjang sumbu minor = 2b = 2√20 = 2(4,47) ≈ 8,94 satuan
b) Untuk mencari koordinat fokus, kita hitung nilai c:
c² = a² – b² = 36 – 20 = 16, maka c = 4
Karena fokus terletak pada sumbu x (karena a² > b²), maka koordinat fokus adalah F₁(-4, 0) dan F₂(4, 0)
c) Eksentrisitas elips = e = c/a = 4/6 = 2/3 ≈ 0,67
Contoh 3: Menentukan Persamaan Elips dengan Pusat di P(h,k)
Tentukan persamaan elips dengan pusat di P(2, -3), sumbu mayor sejajar sumbu x dengan panjang 8, dan sumbu minor dengan panjang 6.
Penyelesaian:
Diketahui pusat elips di P(2, -3) dengan panjang sumbu mayor 8 dan sumbu minor 6.
Maka a = 8/2 = 4 dan b = 6/2 = 3.
Karena sumbu mayor sejajar sumbu x, maka persamaan elips adalah:
$$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$
$$ \frac{(x-2)^2}{16} + \frac{(y+3)^2}{9} = 1 $$
Contoh 4: Menentukan Titik Potong Elips dengan Sumbu Koordinat
Tentukan titik potong elips $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$ dengan sumbu koordinat.
Penyelesaian:
Untuk titik potong dengan sumbu x, substitusi y = 0:
$$ \frac{x^2}{25} + \frac{0^2}{9} = 1 $$
$$ \frac{x^2}{25} = 1 $$
$$ x^2 = 25 $$
$$ x = \pm 5 $$
Jadi, titik potong dengan sumbu x adalah (5, 0) dan (-5, 0).
Untuk titik potong dengan sumbu y, substitusi x = 0:
$$ \frac{0^2}{25} + \frac{y^2}{9} = 1 $$
$$ \frac{y^2}{9} = 1 $$
$$ y^2 = 9 $$
$$ y = \pm 3 $$
Jadi, titik potong dengan sumbu y adalah (0, 3) dan (0, -3).
Contoh 5: Menentukan Luas Elips
Hitunglah luas daerah yang dibatasi oleh elips dengan persamaan $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$.
Penyelesaian:
Dari persamaan $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$, diketahui a² = 16 dan b² = 9.
Maka a = 4 dan b = 3.
Luas elips dihitung dengan rumus L = πab
L = π × 4 × 3 = 12π satuan luas ≈ 37,7 satuan luas.
Kesimpulan
Elips merupakan bentuk geometri penting dengan banyak aplikasi praktis. Pemahaman tentang persamaan dan sifat-sifat elips sangat bermanfaat dalam bidang matematika, fisika, dan teknik. Melalui pendekatan analitis dan geometris, kita dapat mengeksplorasi berbagai aspek elips dan aplikasinya dalam kehidupan nyata.
Sumber dan Referensi
1. Anton, Howard. (2013). Elementary Linear Algebra: Applications Version, 11th Edition. John Wiley & Sons.
2. Leithold, Louis. (2002). The Calculus with Analytic Geometry, 8th Edition. Addison-Wesley.
3. Stewart, James. (2015). Calculus: Early Transcendentals, 8th Edition. Cengage Learning.
4. Purcell, Edwin J., Varberg, Dale E., & Rigdon, Steven E. (2007). Calculus, 9th Edition. Pearson Prentice Hall.
5. Prasolov, V. V., & Tikhomirov, V. M. (2001). Geometry. American Mathematical Society.