Pendahuluan
Trigonometri berasal dari bahasa Yunani, yaitu “trigonon” yang berarti segitiga dan “metron” yang berarti pengukuran. Secara harfiah, trigonometri adalah ilmu yang mempelajari pengukuran segitiga. Dalam matematika modern, trigonometri telah berkembang menjadi bidang yang mempelajari hubungan antara sisi dan sudut segitiga, serta fungsi-fungsi trigonometri seperti sinus, cosinus, dan tangen.
Artikel ini akan menjelaskan konsep dasar trigonometri, rumus-rumus penting, dan aplikasinya dalam kehidupan sehari-hari. Dilengkapi dengan latihan soal dan materi yang bisa diunduh, artikel ini cocok untuk siswa SMA, mahasiswa, atau siapa saja yang ingin memahami trigonometri secara mendalam.
Konsep Dasar Trigonometri
Sudut dan Pengukurannya
Sebelum membahas fungsi trigonometri, penting untuk memahami konsep sudut dan cara pengukurannya. Sudut dapat diukur dalam beberapa satuan:
- Derajat (°) – Satu putaran penuh = 360°
- Radian (rad) – Satu putaran penuh = 2π rad
- Gradian (grad) – Satu putaran penuh = 400 grad
Konversi antara satuan sudut:
- 1° = π/180 rad
- 1 rad = 180°/π
- 1° = 10/9 grad
Fungsi Trigonometri Dasar
Fungsi trigonometri dasar didefinisikan berdasarkan perbandingan sisi-sisi pada segitiga siku-siku:
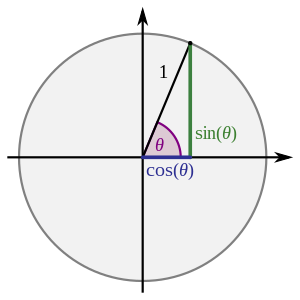
Jika θ adalah sudut dalam segitiga siku-siku dengan sisi miring r, sisi samping x, dan sisi depan y, maka:
- Sinus (sin) = sisi depan / sisi miring = y/r
- Cosinus (cos) = sisi samping / sisi miring = x/r
- Tangen (tan) = sisi depan / sisi samping = y/x = sin θ / cos θ
- Cosecan (csc) = sisi miring / sisi depan = r/y = 1/sin θ
- Secan (sec) = sisi miring / sisi samping = r/x = 1/cos θ
- Cotangen (cot) = sisi samping / sisi depan = x/y = cos θ / sin θ = 1/tan θ
Nilai Fungsi Trigonometri untuk Sudut Istimewa
Berikut adalah tabel nilai fungsi trigonometri untuk sudut-sudut istimewa:
| Sudut (θ) | sin θ | cos θ | tan θ |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | 1/√2 | 1/√2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | ∞ |
Identitas Trigonometri Penting
Identitas trigonometri adalah persamaan yang melibatkan fungsi trigonometri. Berikut adalah beberapa identitas penting:
Identitas Pitagoras
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = csc²θ
Identitas Jumlah dan Selisih Sudut
- sin(A + B) = sin A cos B + cos A sin B
- sin(A – B) = sin A cos B – cos A sin B
- cos(A + B) = cos A cos B – sin A sin B
- cos(A – B) = cos A cos B + sin A sin B
- tan(A + B) = (tan A + tan B) / (1 – tan A tan B)
- tan(A – B) = (tan A – tan B) / (1 + tan A tan B)
Identitas Sudut Rangkap
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ – sin²θ = 2cos²θ – 1 = 1 – 2sin²θ
- tan 2θ = 2 tan θ / (1 – tan²θ)
Aplikasi Trigonometri dalam Kehidupan Sehari-hari
Trigonometri bukan hanya teori matematika yang abstrak, tetapi memiliki banyak aplikasi praktis dalam kehidupan sehari-hari:
1. Arsitektur dan Konstruksi
Arsitek dan insinyur menggunakan trigonometri untuk menghitung tinggi bangunan, kemiringan atap, dan berbagai aspek desain struktural. Misalnya, untuk menghitung tinggi menara dengan sudut elevasi yang diketahui:
Jika seseorang berdiri pada jarak d dari menara dan melihat puncak menara dengan sudut elevasi α, tinggi menara (h) dapat dihitung dengan:
h = d × tan α
Pilot dan navigator menggunakan trigonometri untuk menentukan arah, jarak, dan ketinggian. Dengan menggunakan trigonometri, mereka dapat menghitung:
- Jarak terdekat antara dua titik di permukaan bumi (great-circle distance)
- Arah kompas yang harus diikuti (bearing)
- Waktu tempuh berdasarkan kecepatan dan jarak
3. Astronomi
Trigonometri sangat penting dalam astronomi untuk:
- Menghitung jarak antara benda-benda langit
- Menentukan posisi planet dan bintang
- Memperkirakan ukuran benda langit
4. Elektronika dan Telekomunikasi
Sinyal gelombang elektromagnetik yang digunakan dalam radio, televisi, dan telekomunikasi dapat dimodelkan menggunakan fungsi trigonometri. Fungsi sinus dan cosinus digunakan untuk:
- Modulasi amplitudo (AM) dan modulasi frekuensi (FM)
- Analisis Fourier untuk pemrosesan sinyal
- Rangkaian listrik arus bolak-balik (AC)
5. Fisika
Dalam fisika, trigonometri digunakan untuk:
- Menguraikan gaya menjadi komponen-komponennya
- Menganalisis gerak harmonis sederhana
- Mempelajari gelombang mekanik dan elektromagnetik
Latihan Soal
Soal 1
Hitunglah nilai dari sin 45° + cos 60°.
Soal 2
Sebuah tangga dengan panjang 10 meter disandarkan pada dinding vertikal. Jika tangga membentuk sudut 60° dengan tanah, berapakah tinggi dinding yang dapat dicapai oleh tangga tersebut?
Soal 3
Buktikan bahwa: sin(A + B)sin(A – B) = sin²A – sin²B
Soal 4
Sebuah pesawat terbang pada ketinggian 5000 meter. Dari posisi pesawat, sudut depresi ke titik A di tanah adalah 30°. Berapa jarak horizontal dari titik A ke titik tepat di bawah pesawat?
Soal 5
Jika sin A = 3/5 dan A berada di kuadran I, tentukan nilai dari cos A dan tan A.
Pembahasan Latihan Soal
Pembahasan Soal 1
sin 45° + cos 60° = 1/√2 + 1/2 = 0,707 + 0,5 = 1,207
Pembahasan Soal 2
Diketahui:
- Panjang tangga = 10 meter
- Sudut dengan tanah = 60°
Tinggi dinding yang dicapai = 10 × sin 60° = 10 × (√3/2) = 5√3 ≈ 8,66 meter
Pembahasan Soal 3
Bukti:
sin(A + B)sin(A – B) = (sin A cos B + cos A sin B)(sin A cos B – cos A sin B)
= sin²A cos²B – sin A cos B cos A sin B + cos A sin B sin A cos B – cos²A sin²B
= sin²A cos²B – cos²A sin²B
= sin²A(1 – sin²B) – (1 – sin²A)sin²B
= sin²A – sin²A sin²B – sin²B + sin²A sin²B
= sin²A – sin²B
Pembahasan Soal 4
Diketahui:
- Ketinggian pesawat = 5000 meter
- Sudut depresi = 30°
Sudut elevasi dari titik A ke pesawat juga 30° (sudut berseberangan).
Jarak horizontal = 5000 / tan 30° = 5000 / (1/√3) = 5000 × √3 ≈ 8660 meter
Pembahasan Soal 5
Diketahui:
- sin A = 3/5
- A di kuadran I
Menggunakan identitas Pitagoras:
sin²A + cos²A = 1
(3/5)² + cos²A = 1
9/25 + cos²A = 1
cos²A = 1 – 9/25 = 16/25
cos A = 4/5 (karena A di kuadran I, cos A positif)
Nilai tan A:
tan A = sin A / cos A = (3/5) / (4/5) = 3/4
Materi Terkait
Untuk pemahaman yang lebih mendalam, Anda dapat membaca materi-materi berikut:
- Ringkasan Rumus Trigonometri
- Kumpulan Soal dan Pembahasan Trigonometri
- Latihan Mandiri Trigonometri dengan Kunci Jawaban
Kesimpulan
Trigonometri adalah cabang matematika yang sangat penting dengan berbagai aplikasi dalam kehidupan nyata. Dari arsitektur hingga astronomi, dari navigasi hingga elektronika, konsep-konsep trigonometri banyak digunakan untuk memecahkan masalah praktis.
Dengan memahami konsep dasar, rumus-rumus penting, dan aplikasi trigonometri, Anda akan memiliki fondasi yang kuat untuk mempelajari cabang matematika lainnya seperti kalkulus dan persamaan diferensial.
Jangan lupa untuk berlatih menggunakan soal-soal yang telah disediakan dan mengunduh materi tambahan untuk meningkatkan pemahaman Anda tentang trigonometri.
Artikel ini ditulis oleh Tim PintarMTK. Jika Anda memiliki pertanyaan atau membutuhkan penjelasan lebih lanjut, silakan tinggalkan komentar di bawah artikel ini.