Limit fungsi adalah konsep fundamental dalam kalkulus yang menjadi pondasi untuk memahami turunan dan integral. Artikel ini menyajikan materi limit fungsi lengkap mulai dari pengertian dasar, sifat-sifat penting, rumus-rumus praktis, hingga visualisasi dan contoh soal dengan pembahasannya.
Pengertian Limit Fungsi
Dalam kalkulus dasar, limit fungsi menyatakan nilai yang didekati oleh suatu fungsi ketika variabel bebasnya mendekati suatu nilai tertentu. Secara formal, pengertian limit fungsi $f(x)$ saat $x$ mendekati $a$ ditulis sebagai:
$$\lim_{x \to a} f(x) = L$$
Notasi ini dibaca: “limit $f(x)$ saat $x$ mendekati $a$ adalah $L$.”
Artinya, nilai fungsi $f(x)$ akan semakin mendekati nilai $L$ ketika $x$ semakin dekat (tetapi tidak sama) dengan $a$.
Dalam belajar limit, penting untuk memahami definisi formal menggunakan konsep epsilon delta ($\varepsilon$-$\delta$):
Limit $f(x)$ saat $x$ mendekati $a$ adalah $L$ jika untuk setiap bilangan positif $\varepsilon$ terdapat bilangan positif $\delta$ sehingga:
$$\text{jika } 0 < |x – a| < \delta \text{ maka } |f(x) – L| < \varepsilon$$

Intuisi dan Visualisasi Limit
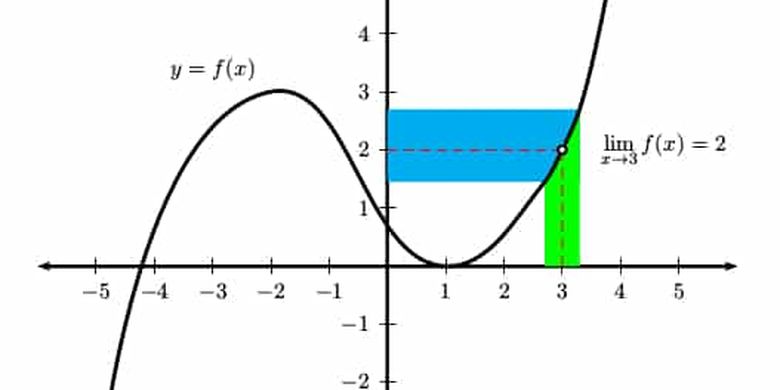
Untuk memahami limit secara intuitif, visualisasi limit sangat membantu. Perhatikan contoh berikut:
Misalkan kita memiliki fungsi $f(x) = \frac{x^2 – 1}{x – 1}$. Fungsi ini tidak terdefinisi saat $x = 1$ karena penyebut bernilai nol. Namun, kita dapat menghitung limit fungsi saat $x$ mendekati 1.
Jika kita coba substitusi nilai $x$ yang semakin mendekati 1, kita akan mendapatkan:
| $x$ mendekati 1 dari kiri | $f(x)$ |
|---|---|
| 0,9 | 1,9 |
| 0,99 | 1,99 |
| 0,999 | 1,999 |
| $x$ mendekati 1 dari kanan | $f(x)$ |
|---|---|
| 1,1 | 2,1 |
| 1,01 | 2,01 |
| 1,001 | 2,001 |
Dari tabel di atas, terlihat bahwa nilai $f(x)$ semakin mendekati 2 saat $x$ mendekati 1 baik dari kiri maupun kanan. Oleh karena itu, $\lim_{x \to 1} f(x) = 2$.
Sifat-Sifat Limit Fungsi
Sifat-sifat limit fungsi sangat memudahkan dalam perhitungan. Berikut adalah sifat-sifat penting yang perlu dikuasai:
- Limit Fungsi Konstan:$$\lim_{x \to a} k = k$$
- Limit Fungsi Identitas:$$\lim_{x \to a} x = a$$
- Limit Penjumlahan/Pengurangan:$$\lim_{x \to a} [f(x) \pm g(x)] = \lim_{x \to a} f(x) \pm \lim_{x \to a} g(x)$$
- Limit Perkalian:$$\lim_{x \to a} [f(x) \cdot g(x)] = \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x)$$
- Limit Pembagian:$$\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)}$$dengan syarat $\lim_{x \to a} g(x) \neq 0$
- Limit Fungsi Pangkat:$$\lim_{x \to a} [f(x)]^n = [\lim_{x \to a} f(x)]^n$$
- Limit Fungsi Komposisi:Jika $\lim_{x \to a} g(x) = L$ dan $f$ kontinu di $L$, maka:$$\lim_{x \to a} f(g(x)) = f(\lim_{x \to a} g(x)) = f(L)$$
Memahami sifat-sifat limit ini sangat penting untuk menyelesaikan berbagai persoalan limit fungsi yang kompleks.
Rumus Limit Fungsi
Berikut adalah beberapa rumus limit khusus yang sering digunakan dalam penyelesaian soal:
1. Limit Bentuk Tak Tentu $\frac{0}{0}$
Jika limit suatu fungsi berbentuk $\frac{0}{0}$, maka dapat diselesaikan dengan:
- Faktorisasi
- Perkalian dengan sekawan
- Aturan L’Hôpital
2. Limit Bentuk Tak Tentu $\frac{\infty}{\infty}$
Untuk limit berbentuk $\frac{\infty}{\infty}$, bagi pembilang dan penyebut dengan variabel pangkat tertinggi.
3. Limit Trigonometri
Limit trigonometri yang penting untuk dihafalkan:
- $$\lim_{x \to 0} \frac{\sin x}{x} = 1$$
- $$\lim_{x \to 0} \frac{\tan x}{x} = 1$$
- $$\lim_{x \to 0} \frac{1-\cos x}{x^2} = \frac{1}{2}$$
4. Limit Bentuk $1^{\infty}$
Untuk limit berbentuk $1^{\infty}$, gunakan rumus:
$$\lim_{x \to a} [f(x)]^{g(x)} = e^{\lim_{x \to a} [g(x) \cdot (f(x)-1)]}$$
5. Limit Tak Hingga
- $$\lim_{x \to \infty} \frac{a_n x^n + a_{n-1}x^{n-1} + \cdots + a_1 x + a_0}{b_m x^m + b_{m-1}x^{m-1} + \cdots + b_1 x + b_0}$$
- Jika $n < m$, maka limit = 0
- Jika $n = m$, maka limit = $\frac{a_n}{b_m}$
- Jika $n > m$, maka limit = $\infty$ atau $-\infty$
Contoh Soal dan Pembahasan
Limit Aljabar
Contoh 1: Limit Aljabar Sederhana
Soal: Tentukan nilai dari $\lim_{x \to 2} (3x^2 – 4x + 1)$
Pembahasan:
Karena fungsi $f(x) = 3x^2 – 4x + 1$ adalah fungsi polinom yang kontinu untuk semua nilai $x$, maka limit aljabar dapat dihitung dengan substitusi langsung:
$$\lim_{x \to 2} (3x^2 – 4x + 1) = 3(2)^2 – 4(2) + 1 = 3(4) – 8 + 1 = 12 – 8 + 1 = 5$$
Jadi, $\lim_{x \to 2} (3x^2 – 4x + 1) = 5$
Contoh 2: Limit Bentuk Tak Tentu $\frac{0}{0}$
Soal: Tentukan nilai dari $\lim_{x \to 3} \frac{x^2 – 9}{x – 3}$
Pembahasan:
Jika kita substitusi langsung $x = 3$, kita akan mendapatkan bentuk tak tentu $\frac{0}{0}$. Oleh karena itu, kita perlu menggunakan faktorisasi:
$$\lim_{x \to 3} \frac{x^2 – 9}{x – 3} = \lim_{x \to 3} \frac{(x-3)(x+3)}{x – 3} = \lim_{x \to 3} (x+3) = 3+3 = 6$$
Jadi, $\lim_{x \to 3} \frac{x^2 – 9}{x – 3} = 6$
Limit Trigonometri
Contoh 3: Limit Trigonometri Dasar
Soal: Tentukan nilai dari $\lim_{x \to 0} \frac{\sin 3x}{x}$
Pembahasan:
Kita dapat menggunakan rumus limit trigonometri $\lim_{x \to 0} \frac{\sin x}{x} = 1$:
$$\lim_{x \to 0} \frac{\sin 3x}{x} = \lim_{x \to 0} \frac{\sin 3x}{3x} \cdot 3 = \lim_{x \to 0} \frac{\sin 3x}{3x} \cdot 3 = 1 \cdot 3 = 3$$
Jadi, $\lim_{x \to 0} \frac{\sin 3x}{x} = 3$

Limit Bentuk Tak Tentu
Contoh 4: Limit dengan Perkalian Sekawan
Soal: Tentukan nilai dari $\lim_{x \to 2} \frac{\sqrt{x+2} – 2}{x-2}$
Pembahasan:
Jika disubstitusi langsung, akan menghasilkan bentuk tak tentu $\frac{0}{0}$. Kita gunakan perkalian dengan sekawan:
$$\lim_{x \to 2} \frac{\sqrt{x+2} – 2}{x-2} = \lim_{x \to 2} \frac{(\sqrt{x+2} – 2)(\sqrt{x+2} + 2)}{(x-2)(\sqrt{x+2} + 2)}$$ $$= \lim_{x \to 2} \frac{(x+2) – 4}{(x-2)(\sqrt{x+2} + 2)}$$ $$= \lim_{x \to 2} \frac{x-2}{(x-2)(\sqrt{x+2} + 2)}$$ $$= \lim_{x \to 2} \frac{1}{\sqrt{x+2} + 2}$$ $$= \frac{1}{\sqrt{2+2} + 2}$$ $$= \frac{1}{4}$$
Jadi, $\lim_{x \to 2} \frac{\sqrt{x+2} – 2}{x-2} = \frac{1}{4}$
Contoh 5: Limit di Tak Hingga
Soal: Tentukan nilai dari $\lim_{x \to \infty} \frac{3x^2 + 2x – 1}{2x^2 – 5x + 3}$
Pembahasan:
Untuk limit di tak hingga, kita bagi pembilang dan penyebut dengan pangkat tertinggi yaitu $x^2$:
$$\lim_{x \to \infty} \frac{3x^2 + 2x – 1}{2x^2 – 5x + 3} = \lim_{x \to \infty} \frac{3 + \frac{2}{x} – \frac{1}{x^2}}{2 – \frac{5}{x} + \frac{3}{x^2}}$$
Saat $x \to \infty$, semua suku dengan $x$ di penyebut akan mendekati 0:
$$\lim_{x \to \infty} \frac{3 + \frac{2}{x} – \frac{1}{x^2}}{2 – \frac{5}{x} + \frac{3}{x^2}} = \frac{3 + 0 – 0}{2 – 0 + 0}$$
$$= \frac{3}{2}$$
Jadi, $\lim_{x \to \infty} \frac{3x^2 + 2x – 1}{2x^2 – 5x + 3} = \frac{3}{2}$
Unduh PDF Materi Limit Fungsi
Untuk mempelajari materi limit secara lebih mendalam, Anda dapat mengunduh PDF materi limit fungsi melalui tautan berikut:
⬇️ Unduh PDF Materi Limit Fungsi
PDF ini berisi:
- Rangkuman materi limit fungsi
- Rumus-rumus penting
- 50+ contoh soal dan pembahasan
- Latihan soal dengan kunci jawaban
Kesimpulan
Materi limit fungsi merupakan konsep fundamental dalam kalkulus yang membantu kita memahami perilaku fungsi saat variabel bebasnya mendekati suatu nilai. Dengan memahami limit, kita dapat mempelajari konsep turunan dan integral yang menjadi dasar dari berbagai aplikasi matematika dalam kehidupan nyata.
Konsep-konsep penting yang perlu diingat dalam belajar limit:
- Limit menyatakan nilai yang didekati fungsi saat variabel bebasnya mendekati suatu nilai
- Limit dapat dihitung dari kiri dan kanan
- Terdapat berbagai teknik untuk menentukan limit, seperti substitusi langsung, faktorisasi, dan aturan L’Hôpital
- Sifat-sifat limit memudahkan perhitungan limit fungsi yang kompleks
Dengan memahami dan menguasai limit fungsi, Anda akan memiliki dasar yang kuat untuk mempelajari konsep-konsep kalkulus lanjutan.
Referensi
- Stewart, J. (2015). Calculus: Early Transcendentals (8th ed.). Cengage Learning.
- Thomas, G. B., Weir, M. D., & Hass, J. (2017). Thomas’ Calculus (14th ed.). Pearson.
- Purcell, E. J., Rigdon, S. E., & Varberg, D. (2007). Calculus (9th ed.). Pearson.