Materi ini membahas cara menentukan persamaan garis singgung pada kurva elips menggunakan berbagai metode. Pemahaman tentang konsep ini penting dalam matematika lanjutan dan aplikasi di bidang fisika, astronomi, dan teknik.
1. Pengertian Garis Singgung Elips
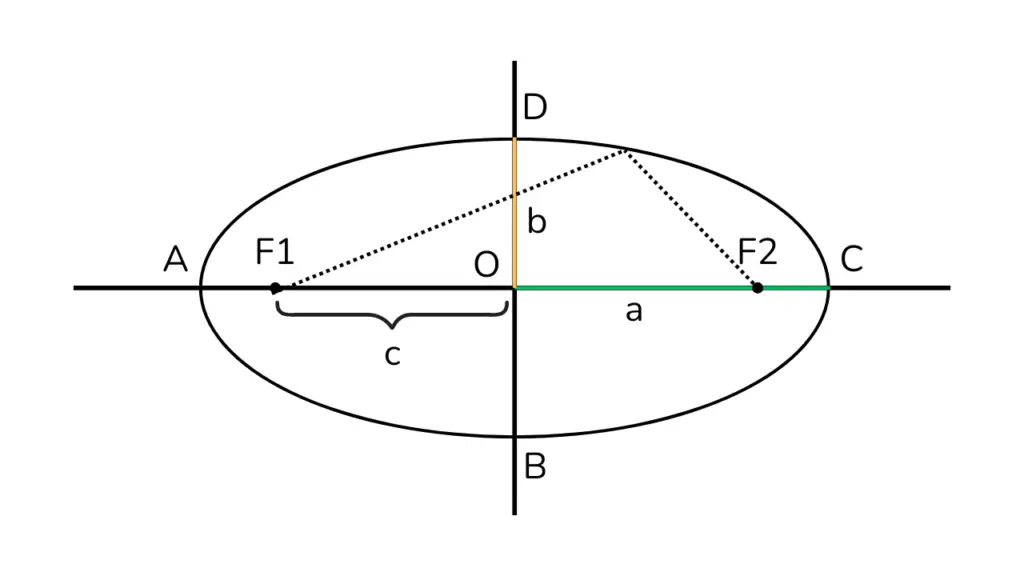
Garis singgung pada elips adalah garis lurus yang menyentuh kurva elips tepat di satu titik. Di titik singgung tersebut, kemiringan (gradien) garis singgung sama dengan kemiringan kurva elips.
2. Metode Menentukan Persamaan Garis Singgung
Ada beberapa metode untuk menentukan persamaan garis singgung pada elips:
2.1 Metode Turunan (Diferensial)
Metode ini menggunakan kalkulus diferensial untuk menentukan gradien kurva di suatu titik, kemudian menggunakan rumus persamaan garis dengan titik dan gradien yang diketahui.
Jika titik $(x_0, y_0)$ terletak pada elips $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, maka:
1. Tentukan $\frac{dy}{dx}$ pada elips dengan mendiferensialkan implisit:
$\frac{d}{dx}\left[\frac{x^2}{a^2} + \frac{y^2}{b^2}\right] = \frac{d}{dx}[1]$
$\frac{2x}{a^2} + \frac{2y}{b^2}\frac{dy}{dx} = 0$
$\frac{dy}{dx} = -\frac{b^2 \cdot x}{a^2 \cdot y}$
2. Gradien di titik $(x_0, y_0)$: $m = -\frac{b^2 \cdot x_0}{a^2 \cdot y_0}$
3. Persamaan garis singgung: $y – y_0 = m(x – x_0)$
Contoh 1: Tentukan persamaan garis singgung elips $\frac{x^2}{9} + \frac{y^2}{4} = 1$ di titik $(0, 2)$.
Penyelesaian:
Pertama, periksa apakah titik $(0, 2)$ terletak pada elips:
$\frac{0^2}{9} + \frac{2^2}{4} = 0 + 1 = 1$ ✓
Gradien di titik $(0, 2)$:
$m = -\frac{4 \cdot 0}{9 \cdot 2} = 0$
Persamaan garis singgung:
$y – 2 = 0(x – 0)$
$y = 2$
Jadi, persamaan garis singgung elips di titik $(0, 2)$ adalah $y = 2$.
2.2 Metode Bentuk Standar
Terdapat rumus langsung untuk menentukan persamaan garis singgung pada elips dalam bentuk standar.
Teorema: Jika titik $P(x_0, y_0)$ terletak pada elips $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, maka persamaan garis singgung di titik $P$ adalah:
$\frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} = 1$
Contoh 2: Tentukan persamaan garis singgung elips $\frac{x^2}{16} + \frac{y^2}{9} = 1$ di titik $(4, 0)$.
Penyelesaian:
Menggunakan rumus $\frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} = 1$:
$\frac{4 \cdot x}{16} + \frac{0 \cdot y}{9} = 1$
$\frac{x}{4} = 1$
$x = 4$
Jadi, persamaan garis singgung elips di titik $(4, 0)$ adalah $x = 4$.
2.3 Metode untuk Titik di Luar Elips
Jika titik $P(x_1, y_1)$ berada di luar elips, maka dapat ditarik dua garis singgung dari titik tersebut ke elips.
Untuk elips $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ dan titik $P(x_1, y_1)$ di luar elips, persamaan garis singgung yang melalui $P$ adalah:
$y = mx + c$ di mana $m$ memenuhi persamaan:
$a^2m^2 + b^2 = (mx_1 – y_1)^2$
atau alternatifnya:
$\frac{(xx_1 – a^2)^2}{a^4} + \frac{(yy_1 – b^2)^2}{b^4} = \frac{x_1^2 – a^2}{a^4} + \frac{y_1^2 – b^2}{b^4}$
Contoh 3: Tentukan persamaan garis singgung elips $\frac{x^2}{25} + \frac{y^2}{16} = 1$ yang melalui titik $(8, 6)$.
Penyelesaian:
Misalkan persamaan garis singgung adalah $y = mx + c$
Titik $(8, 6)$ terletak pada garis ini, sehingga $6 = 8m + c$ atau $c = 6 – 8m$
Substitusi ke persamaan garis: $y = mx + (6 – 8m) = mx – 8m + 6$
Syarat agar garis ini menyinggung elips: $a^2m^2 + b^2 = (mx_1 – y_1)^2$
$25m^2 + 16 = (8m – 6)^2 = 64m^2 – 96m + 36$
$25m^2 + 16 = 64m^2 – 96m + 36$
$-39m^2 + 96m – 20 = 0$
$39m^2 – 96m + 20 = 0$
Dengan rumus ABC: $m = \frac{96 \pm \sqrt{96^2 – 4 \cdot 39 \cdot 20}}{2 \cdot 39} = \frac{96 \pm \sqrt{9216 – 3120}}{78} = \frac{96 \pm \sqrt{6096}}{78}$
$m_1 = 2.0$ dan $m_2 = 0.46$ (dibulatkan)
Untuk $m_1 = 2.0$: $c = 6 – 8 \cdot 2 = 6 – 16 = -10$
Persamaan garis pertama: $y = 2x – 10$
Untuk $m_2 = 0.46$: $c = 6 – 8 \cdot 0.46 = 6 – 3.68 = 2.32$
Persamaan garis kedua: $y = 0.46x + 2.32$
3. Sifat-sifat Khusus Garis Singgung Elips
3.1 Sifat Cermin Elips
Pada titik singgung, sudut antara garis dari fokus ke titik singgung dan garis singgung sama dengan sudut antara garis singgung dan garis dari titik singgung ke fokus lainnya.
Fakta penting: Sifat ini digunakan dalam desain ruang berbisik (whispering gallery) dan antena parabola.
3.2 Garis Singgung pada Titik Ujung
Garis singgung pada ujung sumbu mayor dan minor elips memiliki sifat khusus:
- Di ujung sumbu mayor $(±a, 0)$: garis singgung tegak lurus sumbu $x$ $(x = ±a)$
- Di ujung sumbu minor $(0, ±b)$: garis singgung tegak lurus sumbu $y$ $(y = ±b)$
4. Soal-soal Latihan
Soal 1
Tentukan persamaan garis singgung elips $\frac{x^2}{16} + \frac{y^2}{9} = 1$ di titik $(2\sqrt{2}, \frac{3\sqrt{2}}{2})$.
Pembahasan:
Periksa apakah titik berada pada elips:
$\frac{(2\sqrt{2})^2}{16} + \frac{(3\sqrt{2}/2)^2}{9} = \frac{8}{16} + \frac{9/2}{9} = \frac{1}{2} + \frac{1}{2} = 1$ ✓
Menggunakan rumus $\frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} = 1$:
$\frac{2\sqrt{2} \cdot x}{16} + \frac{3\sqrt{2}/2 \cdot y}{9} = 1$
$\frac{\sqrt{2}x}{8} + \frac{\sqrt{2}y}{6} = 1$
$\frac{x}{8} + \frac{y}{6} = \frac{1}{\sqrt{2}}$
$\frac{3x}{24} + \frac{4y}{24} = \frac{1}{\sqrt{2}}$
$3x + 4y = 24 / \sqrt{2}$
$3x + 4y = 12\sqrt{2}$
Jadi, persamaan garis singgung adalah $3x + 4y = 12\sqrt{2}$
Soal 2
Tentukan persamaan garis singgung elips $4x^2 + 9y^2 = 36$ yang sejajar dengan garis $2x – y + 5 = 0$.
Pembahasan:
Ubah bentuk elips ke bentuk standar: $\frac{x^2}{9} + \frac{y^2}{4} = 1$
Sehingga $a = 3$ dan $b = 2$
Gradien garis $2x – y + 5 = 0$ adalah $m_1 = 2$
Garis singgung yang dicari harus memiliki gradien yang sama, yaitu $m = 2$
Jika titik singgung adalah $(x_0, y_0)$, maka:
Gradien di titik tersebut: $-\frac{b^2x_0}{a^2y_0} = -\frac{4x_0}{9y_0} = 2$
$4x_0 = -18y_0$
$x_0 = -\frac{9y_0}{2}$
Karena $(x_0, y_0)$ terletak pada elips:
$\frac{x_0^2}{9} + \frac{y_0^2}{4} = 1$
$\frac{(-9y_0/2)^2}{9} + \frac{y_0^2}{4} = 1$
$\frac{81y_0^2/4}{9} + \frac{y_0^2}{4} = 1$
$\frac{9y_0^2}{4} + \frac{y_0^2}{4} = 1$
$\frac{10y_0^2}{4} = 1$
$y_0^2 = \frac{4}{10} = \frac{2}{5}$
$y_0 = \pm\sqrt{\frac{2}{5}}$
Untuk $y_0 = \sqrt{\frac{2}{5}}$, $x_0 = -\frac{9}{2} \cdot \sqrt{\frac{2}{5}} = -\frac{9\sqrt{10}}{10}$
Untuk $y_0 = -\sqrt{\frac{2}{5}}$, $x_0 = -\frac{9}{2} \cdot (-\sqrt{\frac{2}{5}}) = \frac{9\sqrt{10}}{10}$
Persamaan garis singgung di titik $(x_0, y_0)$: $y – y_0 = m(x – x_0)$
Untuk titik $(-\frac{9\sqrt{10}}{10}, \sqrt{\frac{2}{5}})$:
$y – \sqrt{\frac{2}{5}} = 2(x + \frac{9\sqrt{10}}{10})$
$y – \sqrt{\frac{2}{5}} = 2x + \frac{18\sqrt{10}}{10}$
$y = 2x + \frac{18\sqrt{10}}{10} + \sqrt{\frac{2}{5}}$
$y = 2x + \frac{18\sqrt{10}}{10} + \frac{\sqrt{10}}{\sqrt{5}} = 2x + \frac{18\sqrt{10} + 10\sqrt{2}}{10}$
Untuk titik $(\frac{9\sqrt{10}}{10}, -\sqrt{\frac{2}{5}})$:
$y + \sqrt{\frac{2}{5}} = 2(x – \frac{9\sqrt{10}}{10})$
$y + \sqrt{\frac{2}{5}} = 2x – \frac{18\sqrt{10}}{10}$
$y = 2x – \frac{18\sqrt{10}}{10} – \sqrt{\frac{2}{5}}$
$y = 2x – \frac{18\sqrt{10} + 10\sqrt{2}}{10}$
Jadi, persamaan garis singgung yang sejajar dengan $2x – y + 5 = 0$ adalah:
$y = 2x + \frac{18\sqrt{10} + 10\sqrt{2}}{10}$ atau $y = 2x – \frac{18\sqrt{10} + 10\sqrt{2}}{10}$
Soal 3
Tentukan persamaan garis singgung elips $\frac{x^2}{25} + \frac{y^2}{9} = 1$ yang tegak lurus dengan garis $3x + 4y – 12 = 0$.
Pembahasan:
Gradien garis $3x + 4y – 12 = 0$ adalah $m_1 = -\frac{3}{4}$
Garis singgung yang dicari tegak lurus dengan garis tersebut, sehingga gradiennya adalah:
$m = -\frac{1}{m_1} = -\frac{1}{(-\frac{3}{4})} = \frac{4}{3}$
Jika titik singgung adalah $(x_0, y_0)$, maka:
$-\frac{b^2x_0}{a^2y_0} = -\frac{9x_0}{25y_0} = \frac{4}{3}$
$\frac{9x_0}{25y_0} = -\frac{4}{3}$
$9x_0 = -\frac{4 \cdot 25y_0}{3}$
$9x_0 = -\frac{100y_0}{3}$
$x_0 = -\frac{100y_0}{27}$
Karena $(x_0, y_0)$ terletak pada elips:
$\frac{x_0^2}{25} + \frac{y_0^2}{9} = 1$
$\frac{(-100y_0/27)^2}{25} + \frac{y_0^2}{9} = 1$
$\frac{10000y_0^2/729}{25} + \frac{y_0^2}{9} = 1$
$\frac{10000y_0^2}{729 \cdot 25} + \frac{y_0^2}{9} = 1$
$\frac{400y_0^2}{729} + \frac{y_0^2}{9} = 1$
$\frac{400y_0^2}{729} + \frac{81y_0^2}{729} = 1$
$\frac{481y_0^2}{729} = 1$
$y_0^2 = \frac{729}{481}$
$y_0 = \pm\sqrt{\frac{729}{481}}$
Diperoleh persamaan garis singgung yang tegak lurus dengan $3x + 4y – 12 = 0$.
5. Aplikasi dalam Kehidupan Nyata
Konsep garis singgung elips digunakan dalam berbagai aplikasi, seperti:
- Desain lensa dan cermin optik
- Galeri berbisik (whispering gallery) dengan bentuk elips
- Orbit planet dan benda langit lainnya
- Teknik perhitungan dalam astronomi
- Litotripsi gelombang kejut (penghancuran batu ginjal)