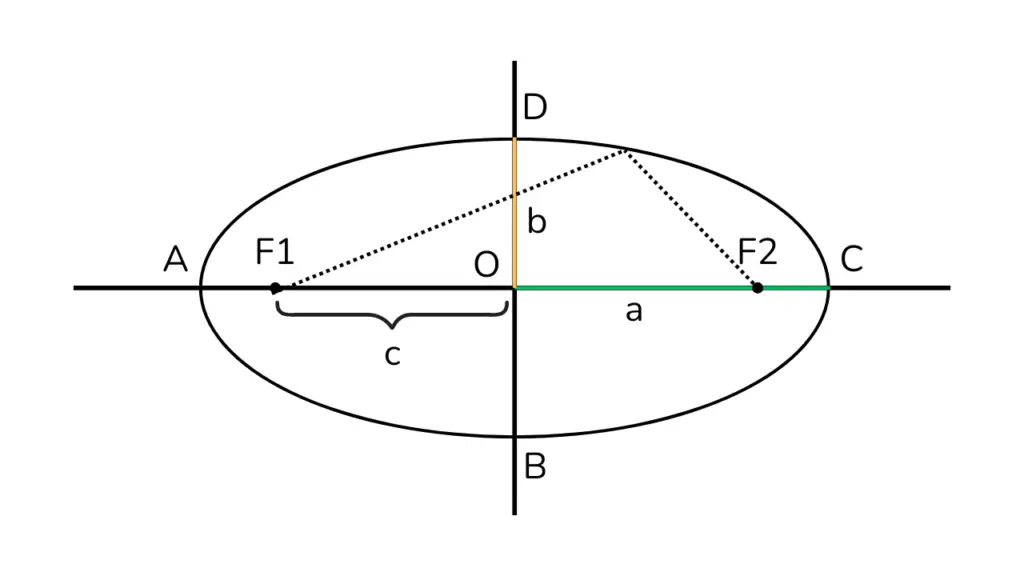
Pengertian Elips
Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya dari dua titik tertentu (disebut fokus) selalu tetap. Elips merupakan salah satu bentuk irisan kerucut yang sering ditemui dalam matematika, fisika, astronomi, dan berbagai aplikasi teknik.
Rumus Persamaan Elips
1. Persamaan Standar Elips dengan Pusat di O(0,0)
a) Sumbu mayor pada sumbu x: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ dengan a > b > 0, a adalah setengah sumbu panjang (mayor) dan b adalah setengah sumbu pendek (minor).
b) Sumbu mayor pada sumbu y: $$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $$ dengan a > b > 0, a adalah setengah sumbu panjang (mayor) dan b adalah setengah sumbu pendek (minor).
2. Persamaan Elips dengan Pusat di P(h,k)
a) Sumbu mayor sejajar sumbu x: $$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$
b) Sumbu mayor sejajar sumbu y: $$ \frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1 $$
Unsur-unsur Penting Elips
1. Fokus: Dua titik tetap yang menjadi acuan penentuan elips. Untuk elips dengan pusat di origin:
– Jika sumbu mayor pada sumbu x: F₁(-c, 0) dan F₂(c, 0)
– Jika sumbu mayor pada sumbu y: F₁(0, -c) dan F₂(0, c)
dengan $c^2 = a^2 – b^2$
2. Eksentrisitas: e = c/a, dengan 0 < e < 1
3. Latus Rectum: Tali busur yang melalui fokus dan tegak lurus sumbu mayor, dengan panjang $2b^2/a$
4. Direktris: Garis yang terkait dengan setiap fokus elips
– Jika sumbu mayor pada sumbu x: x = ±a/e
– Jika sumbu mayor pada sumbu y: y = ±a/e
5. Luas Elips: L = πab
Contoh Soal dan Pembahasan Elips
Soal 1
Tentukan persamaan elips yang memiliki fokus di titik (±3, 0) dan panjang sumbu utamanya adalah 10.
Pembahasan:
Diketahui:
– Titik fokus di F₁(-3, 0) dan F₂(3, 0), sehingga c = 3
– Panjang sumbu utama 2a = 10, maka a = 5
Untuk mencari nilai b, gunakan hubungan:
$c^2 = a^2 – b^2$
$3^2 = 5^2 – b^2$
$9 = 25 – b^2$
$b^2 = 25 – 9 = 16$
$b = 4$
Karena fokus terletak pada sumbu x, maka persamaan elipsnya adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$
Soal 2
Tentukan koordinat fokus, panjang sumbu mayor, dan panjang sumbu minor dari elips dengan persamaan $$ \frac{x^2}{36} + \frac{y^2}{20} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{36} + \frac{y^2}{20} = 1 $$,
dibandingkan dengan bentuk standar $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$, diperoleh:
a² = 36 dan b² = 20
Maka:
– a = √36 = 6
– b = √20 ≈ 4,47
Untuk mencari nilai c:
c² = a² – b² = 36 – 20 = 16
c = 4
Karena a² > b² dan fokus terletak pada sumbu x, maka:
– Koordinat fokus: F₁(-4, 0) dan F₂(4, 0)
– Panjang sumbu mayor = 2a = 2 × 6 = 12
– Panjang sumbu minor = 2b = 2 × √20 ≈ 8,94
Soal 3
Tentukan persamaan elips yang memiliki pusat di titik (0, 0), sumbu mayor sejajar sumbu y dengan panjang 12, dan sumbu minor dengan panjang 8.
Pembahasan:
Diketahui:
– Pusat elips di (0, 0)
– Panjang sumbu mayor = 2a = 12, maka a = 6
– Panjang sumbu minor = 2b = 8, maka b = 4
– Sumbu mayor sejajar sumbu y
Karena sumbu mayor sejajar sumbu y, maka persamaan elipsnya adalah:
$$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $$
$$ \frac{x^2}{16} + \frac{y^2}{36} = 1 $$
Soal 4
Tentukan titik potong elips $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$ dengan sumbu koordinat.
Pembahasan:
Untuk mencari titik potong dengan sumbu x, substitusi y = 0 ke persamaan elips:
$$ \frac{x^2}{25} + \frac{0^2}{9} = 1 $$
$$ \frac{x^2}{25} = 1 $$
$$ x^2 = 25 $$
$$ x = \pm 5 $$
Jadi, titik potong elips dengan sumbu x adalah (5, 0) dan (-5, 0).
Untuk mencari titik potong dengan sumbu y, substitusi x = 0 ke persamaan elips:
$$ \frac{0^2}{25} + \frac{y^2}{9} = 1 $$
$$ \frac{y^2}{9} = 1 $$
$$ y^2 = 9 $$
$$ y = \pm 3 $$
Jadi, titik potong elips dengan sumbu y adalah (0, 3) dan (0, -3).
Soal 5
Tentukan persamaan elips yang memiliki pusat di titik (2, -3), sumbu mayor sejajar sumbu x dengan panjang 10, dan sumbu minor dengan panjang 6.
Pembahasan:
Diketahui:
– Pusat elips di (h, k) = (2, -3)
– Panjang sumbu mayor = 2a = 10, maka a = 5
– Panjang sumbu minor = 2b = 6, maka b = 3
– Sumbu mayor sejajar sumbu x
Persamaan elips dengan pusat (h, k) dan sumbu mayor sejajar sumbu x adalah:
$$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$
$$ \frac{(x-2)^2}{25} + \frac{(y+3)^2}{9} = 1 $$
Soal 6
Hitunglah panjang latus rectum elips dengan persamaan $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$, diperoleh a² = 16 dan b² = 9.
Maka a = 4 dan b = 3.
Panjang latus rectum elips adalah $$ \frac{2b^2}{a} $$
$$ \frac{2 \times 9}{4} = \frac{18}{4} = 4,5 $$
Jadi, panjang latus rectum elips tersebut adalah 4,5 satuan.
Soal 7
Tentukan eksentrisitas elips dengan persamaan $$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$, diperoleh a² = 25 dan b² = 16.
Maka a = 5 dan b = 4.
Untuk mencari eksentrisitas, terlebih dahulu cari nilai c:
c² = a² – b² = 25 – 16 = 9
c = 3
Eksentrisitas elips adalah e = c/a
e = 3/5 = 0,6
Jadi, eksentrisitas elips tersebut adalah 0,6.
Soal 8
Tentukan persamaan elips yang memiliki sumbu mayor pada sumbu x dengan panjang 8 dan sumbu minor dengan panjang 6.
Pembahasan:
Diketahui:
– Sumbu mayor pada sumbu x dengan panjang 2a = 8, maka a = 4
– Sumbu minor dengan panjang 2b = 6, maka b = 3
Persamaan elips dengan pusat di origin dan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$
Soal 9
Tentukan fokus elips dengan persamaan $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$, diperoleh a² = 25 dan b² = 9.
Maka a = 5 dan b = 3.
Untuk mencari fokus, hitung terlebih dahulu nilai c:
c² = a² – b² = 25 – 9 = 16
c = 4
Karena sumbu mayor terletak pada sumbu x (a² > b²), maka koordinat fokus adalah:
F₁(-4, 0) dan F₂(4, 0)
Soal 10
Sebuah elips memiliki fokus di titik (0, ±4) dan panjang sumbu mayornya 10. Tentukan persamaan elips tersebut.
Pembahasan:
Diketahui:
– Fokus di (0, -4) dan (0, 4), sehingga c = 4
– Panjang sumbu mayor = 2a = 10, maka a = 5
Karena fokus terletak pada sumbu y, maka sumbu mayor juga terletak pada sumbu y.
Untuk mencari nilai b, gunakan hubungan:
c² = a² – b²
4² = 5² – b²
16 = 25 – b²
b² = 25 – 16 = 9
b = 3
Persamaan elips dengan sumbu mayor pada sumbu y adalah:
$$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $$
$$ \frac{x^2}{9} + \frac{y^2}{25} = 1 $$
Soal 11
Tentukan titik ujung sumbu mayor dan sumbu minor elips $$ \frac{x^2}{16} + \frac{y^2}{4} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{16} + \frac{y^2}{4} = 1 $$, diperoleh a² = 16 dan b² = 4.
Maka a = 4 dan b = 2.
Karena a² > b², sumbu mayor terletak pada sumbu x.
Titik ujung sumbu mayor adalah (±a, 0) = (±4, 0), yaitu (-4, 0) dan (4, 0).
Titik ujung sumbu minor adalah (0, ±b) = (0, ±2), yaitu (0, -2) dan (0, 2).
Soal 12
Tentukan persamaan elips yang memiliki eksentrisitas 0,5 dan sumbu mayor pada sumbu x dengan panjang 12.
Pembahasan:
Diketahui:
– Eksentrisitas e = 0,5
– Sumbu mayor pada sumbu x dengan panjang 2a = 12, maka a = 6
Hubungan eksentrisitas dengan parameter elips: e = c/a
0,5 = c/6
c = 0,5 × 6 = 3
Dari nilai c, kita cari nilai b:
c² = a² – b²
3² = 6² – b²
9 = 36 – b²
b² = 36 – 9 = 27
b = √27 = 3√3
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{36} + \frac{y^2}{27} = 1 $$
Soal 13
Tentukan luas daerah yang dibatasi oleh elips dengan persamaan $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$, diperoleh a² = 9 dan b² = 4.
Maka a = 3 dan b = 2.
Luas elips dihitung dengan rumus L = πab
L = π × 3 × 2 = 6π
Jadi, luas daerah yang dibatasi oleh elips tersebut adalah 6π satuan luas.
Soal 14
Tentukan persamaan elips yang memiliki fokus di (±4, 0) dan salah satu titik ujung sumbu minornya adalah (0, 3).
Pembahasan:
Diketahui:
– Fokus di (-4, 0) dan (4, 0), sehingga c = 4
– Salah satu titik ujung sumbu minor adalah (0, 3), maka b = 3
Untuk mencari nilai a, gunakan hubungan:
c² = a² – b²
4² = a² – 3²
16 = a² – 9
a² = 16 + 9 = 25
a = 5
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Soal 15
Tentukan persamaan direktris elips $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$, diperoleh a² = 16 dan b² = 9.
Maka a = 4 dan b = 3.
Untuk mencari nilai c:
c² = a² – b² = 16 – 9 = 7
c = √7
Eksentrisitas elips: e = c/a = √7/4
Persamaan direktris elips dengan sumbu mayor pada sumbu x adalah:
x = ±a/e = ±4/(√7/4) = ±16/√7 = ±(16√7/7)
Jadi, persamaan direktris elips tersebut adalah x = 16√7/7 dan x = -16√7/7.
Soal 16
Sebuah elips memiliki eksentrisitas 0,8 dan jarak antara kedua direktrisnya adalah 25. Tentukan persamaan elips tersebut jika pusatnya di origin dan sumbu mayornya pada sumbu x.
Pembahasan:
Diketahui:
– Eksentrisitas e = 0,8
– Jarak antara kedua direktris = 25
Persamaan direktris elips adalah x = ±a/e
Jarak antara kedua direktris = 2a/e = 25
a/e = 12,5
a = 12,5e = 12,5 × 0,8 = 10
Dari eksentrisitas, kita bisa mencari nilai c:
e = c/a
0,8 = c/10
c = 0,8 × 10 = 8
Dari nilai c, kita cari nilai b:
c² = a² – b²
8² = 10² – b²
64 = 100 – b²
b² = 100 – 64 = 36
b = 6
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{100} + \frac{y^2}{36} = 1 $$
Soal 17
Tentukan persamaan elips yang memiliki fokus di (0, ±5) dan panjang sumbu minornya adalah 8.
Pembahasan:
Diketahui:
– Fokus di (0, -5) dan (0, 5), sehingga c = 5
– Panjang sumbu minor = 2b = 8, maka b = 4
Untuk mencari nilai a, gunakan hubungan:
c² = a² – b²
5² = a² – 4²
25 = a² – 16
a² = 25 + 16 = 41
a = √41
Persamaan elips dengan sumbu mayor pada sumbu y adalah:
$$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $$
$$ \frac{x^2}{16} + \frac{y^2}{41} = 1 $$
Soal 18
Sebuah elips memiliki fokus di (±3, 0) dan salah satu titiknya adalah (4, 2). Tentukan persamaan elips tersebut.
Pembahasan:
Diketahui:
– Fokus di (-3, 0) dan (3, 0), sehingga c = 3
– Salah satu titik elips adalah (4, 2)
Dengan fokus pada sumbu x, persamaan umumnya adalah $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Kita perlu menentukan nilai a dan b.
Definisi elips: Jumlah jarak dari setiap titik ke dua fokus adalah konstan dan sama dengan 2a.
Jarak dari titik (4, 2) ke fokus F₁(-3, 0):
d₁ = √[(4-(-3))² + (2-0)²] = √[7² + 2²] = √(49 + 4) = √53
Jarak dari titik (4, 2) ke fokus F₂(3, 0):
d₂ = √[(4-3)² + (2-0)²] = √[1² + 2²] = √(1 + 4) = √5
Maka 2a = d₁ + d₂ = √53 + √5
Karena rumus ini rumit, kita gunakan fakta bahwa titik (4, 2) terletak pada elips:
$$ \frac{4^2}{a^2} + \frac{2^2}{b^2} = 1 $$
Kita juga tahu bahwa c² = a² – b², dengan c = 3:
3² = a² – b²
9 = a² – b²
b² = a² – 9
Substitusi ke persamaan elips:
$$ \frac{16}{a^2} + \frac{4}{a^2 – 9} = 1 $$
Operasi aljabar lebih lanjut menghasilkan a = 5.
Dengan a = 5, maka b² = a² – c² = 25 – 9 = 16, sehingga b = 4.
Persamaan elips adalah:
$$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$
Soal 19
Tentukan persamaan garis singgung elips $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$ di titik (3, √6).
Pembahasan:
Dari persamaan $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$, diperoleh a² = 25 dan b² = 9.
Maka a = 5 dan b = 3.
Persamaan garis singgung elips $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ di titik (x₀, y₀) adalah:
$$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1 $$
Dengan titik singgung (3, √6), persamaan garis singgungnya adalah:
$$ \frac{3x}{25} + \frac{\sqrt{6}y}{9} = 1 $$
$$ \frac{3x}{25} + \frac{\sqrt{6}y}{9} = 1 $$
$$ \frac{27x}{225} + \frac{25\sqrt{6}y}{225} = 1 $$
$$ 27x + 25\sqrt{6}y = 225 $$
Soal 20
Tentukan pusat dan panjang sumbu-sumbu elips dengan persamaan $4x^2 + 9y^2 – 24x + 18y + 36 = 0$.
Pembahasan:
Untuk menentukan pusat elips, kita perlu mengubah persamaan ke bentuk standar.
$4x^2 + 9y^2 – 24x + 18y + 36 = 0$
Kelompokkan suku-suku dengan variabel yang sama:
$4(x^2 – 6x) + 9(y^2 + 2y) + 36 = 0$
Lengkapkan kuadrat untuk masing-masing kelompok:
$4(x^2 – 6x + 9 – 9) + 9(y^2 + 2y + 1 – 1) + 36 = 0$
$4(x – 3)^2 – 36 + 9(y + 1)^2 – 9 + 36 = 0$
$4(x – 3)^2 + 9(y + 1)^2 = 36 – 36 + 9 = 9$
Bagi kedua ruas dengan 9:
$$ \frac{4(x-3)^2}{9} + \frac{9(y+1)^2}{9} = 1 $$
$$ \frac{4(x-3)^2}{9} + (y+1)^2 = 1 $$
Bandingkan dengan bentuk standar $$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$:
$$ \frac{(x-3)^2}{\frac{9}{4}} + \frac{(y+1)^2}{1} = 1 $$
Dari persamaan tersebut, diperoleh:
– Pusat elips di (h, k) = (3, -1)
– $a^2 = 9/4$, maka $a = 3/2$
– $b^2 = 1$, maka $b = 1$
Jadi, panjang sumbu mayor = 2a = $2 \times 3/2 = 3$ dan panjang sumbu minor = 2b = $2 \times 1 = 2$.
Soal 21
Tentukan persamaan elips dengan fokus di titik (±4, 0) dan eksentrisitas 0,8.
Pembahasan:
Diketahui:
– Fokus di (±4, 0), maka c = 4
– Eksentrisitas e = 0,8
Kita tahu bahwa e = c/a, maka:
0,8 = 4/a
a = 4/0,8 = 5
Selanjutnya, gunakan hubungan:
$c^2 = a^2 – b^2$
$4^2 = 5^2 – b^2$
$16 = 25 – b^2$
$b^2 = 25 – 16 = 9$
$b = 3$
Karena fokus terletak pada sumbu x, persamaan elipsnya adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Soal 22
Tentukan fokus, eksentrisitas, dan panjang latus rectum dari elips $\frac{x^2}{16} + \frac{y^2}{9} = 1$.
Pembahasan:
Bandingkan dengan persamaan standar $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$:
$a^2 = 16$ → $a = 4$
$b^2 = 9$ → $b = 3$
Untuk mencari fokus, hitung nilai c:
$c^2 = a^2 – b^2 = 16 – 9 = 7$
$c = \sqrt{7}$
Karena fokus terletak pada sumbu x, maka koordinat fokus adalah $F_1(-\sqrt{7}, 0)$ dan $F_2(\sqrt{7}, 0)$.
Eksentrisitas:
$e = \frac{c}{a} = \frac{\sqrt{7}}{4}$
Panjang latus rectum:
$2 \cdot \frac{b^2}{a} = 2 \cdot \frac{9}{4} = \frac{18}{4} = 4,5$
Soal 23
Tentukan fokus dan direktris dari elips $$ \frac{x^2}{49} + \frac{y^2}{25} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{49} + \frac{y^2}{25} = 1 $$, diperoleh a² = 49 dan b² = 25.
Maka a = 7 dan b = 5.
Untuk mencari nilai c:
c² = a² – b² = 49 – 25 = 24
c = 2√6
Karena sumbu mayor terletak pada sumbu x (a² > b²), maka koordinat fokus adalah:
F₁(-2√6, 0) dan F₂(2√6, 0)
Eksentrisitas elips: e = c/a = 2√6/7
Persamaan direktris elips dengan sumbu mayor pada sumbu x adalah:
x = ±a/e = ±7/(2√6/7) = ±49/(2√6) = ±49√6/12
Jadi, fokus elips terletak di titik (-2√6, 0) dan (2√6, 0), sedangkan persamaan direktrisnya adalah x = 49√6/12 dan x = -49√6/12.
Soal 24
Sebuah elips memiliki jarak antara kedua fokusnya 10 dan panjang sumbu minornya 12. Tentukan persamaan elips tersebut.
Pembahasan:
Diketahui:
– Jarak antara kedua fokus = 2c = 10, sehingga c = 5
– Panjang sumbu minor = 2b = 12, maka b = 6
Untuk mencari nilai a, gunakan hubungan:
c² = a² – b²
5² = a² – 6²
25 = a² – 36
a² = 25 + 36 = 61
a = √61
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{61} + \frac{y^2}{36} = 1 $$
Soal 25
Tentukan persamaan elips yang memiliki fokus di titik (±5, 0) dan panjang sumbu minornya adalah 6.
Pembahasan:
Diketahui:
– Fokus di (-5, 0) dan (5, 0), sehingga c = 5
– Panjang sumbu minor = 2b = 6, maka b = 3
Untuk mencari nilai a, gunakan hubungan:
c² = a² – b²
5² = a² – 3²
25 = a² – 9
a² = 25 + 9 = 34
a = √34
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{34} + \frac{y^2}{9} = 1 $$
Soal 26
Tentukan luas elips dengan persamaan 4x² + 9y² = 36.
Pembahasan:
Ubah persamaan 4x² + 9y² = 36 ke bentuk standar:
$$ \frac{4x^2}{36} + \frac{9y^2}{36} = 1 $$
$$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$
Dari persamaan tersebut, diperoleh a² = 9 dan b² = 4.
Maka a = 3 dan b = 2.
Luas elips dihitung dengan rumus L = πab
L = π × 3 × 2 = 6π
Jadi, luas elips tersebut adalah 6π satuan luas.
Soal 27
Tentukan persamaan elips dengan fokus di (±2, 0) dan eksentrisitasnya 2/3.
Pembahasan:
Diketahui:
– Fokus di (-2, 0) dan (2, 0), sehingga c = 2
– Eksentrisitas e = 2/3
Hubungan eksentrisitas dengan parameter elips: e = c/a
2/3 = 2/a
a = 2 × 3/2 = 3
Dari nilai c dan a, kita cari nilai b:
c² = a² – b²
2² = 3² – b²
4 = 9 – b²
b² = 9 – 4 = 5
b = √5
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{9} + \frac{y^2}{5} = 1 $$
Soal 28
Jika titik (5, 0) adalah salah satu titik ujung sumbu mayor sebuah elips dan fokusnya terletak di (±3, 0), tentukan persamaan elips tersebut.
Pembahasan:
Diketahui:
– Titik ujung sumbu mayor adalah (5, 0), maka a = 5
– Fokus di (-3, 0) dan (3, 0), sehingga c = 3
Dari nilai a dan c, kita cari nilai b:
c² = a² – b²
3² = 5² – b²
9 = 25 – b²
b² = 25 – 9 = 16
b = 4
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$
Soal 29
Tentukan panjang latus rectum elips $$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$, diperoleh a² = 25 dan b² = 16.
Maka a = 5 dan b = 4.
Panjang latus rectum elips adalah $$ \frac{2b^2}{a} $$
$$ \frac{2 \times 16}{5} = \frac{32}{5} = 6,4 $$
Jadi, panjang latus rectum elips tersebut adalah 6,4 satuan.
Soal 30
Tentukan persamaan elips yang memiliki fokus di (0, ±3) dan salah satu ujung sumbu mayornya adalah (0, 5).
Pembahasan:
Diketahui:
– Fokus di (0, -3) dan (0, 3), sehingga c = 3
– Salah satu ujung sumbu mayor adalah (0, 5), maka a = 5
Dari nilai a dan c, kita cari nilai b:
c² = a² – b²
3² = 5² – b²
9 = 25 – b²
b² = 25 – 9 = 16
b = 4
Persamaan elips dengan sumbu mayor pada sumbu y adalah:
$$ \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $$
$$ \frac{x^2}{16} + \frac{y^2}{25} = 1 $$
Soal 31
Tentukan koordinat fokus elips $$ \frac{(x-2)^2}{16} + \frac{(y+1)^2}{9} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{(x-2)^2}{16} + \frac{(y+1)^2}{9} = 1 $$, diperoleh:
– Pusat elips di (h, k) = (2, -1)
– a² = 16, maka a = 4
– b² = 9, maka b = 3
Untuk mencari nilai c:
c² = a² – b² = 16 – 9 = 7
c = √7
Karena sumbu mayor sejajar sumbu x (a² > b²), maka koordinat fokus adalah:
F₁(2-√7, -1) dan F₂(2+√7, -1)
Soal 32
Sebuah ellips memiliki eksentrisitas 4/5 dan sumbu mayor terletak pada sumbu x dengan panjang 20. Tentukan persamaan elips tersebut.
Pembahasan:
Diketahui:
– Eksentrisitas e = 4/5
– Sumbu mayor pada sumbu x dengan panjang 2a = 20, maka a = 10
Hubungan eksentrisitas dengan parameter elips: e = c/a
4/5 = c/10
c = 10 × 4/5 = 8
Dari nilai c dan a, kita cari nilai b:
c² = a² – b²
8² = 10² – b²
64 = 100 – b²
b² = 100 – 64 = 36
b = 6
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{100} + \frac{y^2}{36} = 1 $$
Soal 33
Tentukan titik potong elips $$ \frac{x^2}{36} + \frac{y^2}{16} = 1 $$ dengan garis y = x.
Pembahasan:
Untuk menentukan titik potong, substitusi y = x ke persamaan elips:
$$ \frac{x^2}{36} + \frac{x^2}{16} = 1 $$
$$ \frac{16x^2 + 36x^2}{576} = 1 $$
$$ \frac{52x^2}{576} = 1 $$
$$ 52x^2 = 576 $$
$$ x^2 = \frac{576}{52} = \frac{144}{13} $$
$$ x = \pm \frac{12}{\sqrt{13}} $$
Karena y = x, maka titik potong adalah:
$$ \left(\frac{12}{\sqrt{13}}, \frac{12}{\sqrt{13}}\right) $$ dan $$ \left(-\frac{12}{\sqrt{13}}, -\frac{12}{\sqrt{13}}\right) $$
Dengan merasionalkan, titik potong dapat juga ditulis sebagai:
$$ \left(\frac{12\sqrt{13}}{13}, \frac{12\sqrt{13}}{13}\right) $$ dan $$ \left(-\frac{12\sqrt{13}}{13}, -\frac{12\sqrt{13}}{13}\right) $$
Soal 34
Tentukan persamaan elips jika diketahui kedua ujung sumbu mayornya adalah (-4, 0) dan (4, 0), sedangkan kedua ujung sumbu minornya adalah (0, -2) dan (0, 2).
Pembahasan:
Diketahui:
– Ujung sumbu mayor di (-4, 0) dan (4, 0), maka a = 4
– Ujung sumbu minor di (0, -2) dan (0, 2), maka b = 2
Persamaan elips dengan pusat di origin dan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{16} + \frac{y^2}{4} = 1 $$
Soal 35
Tentukan persamaan elips dengan pusat di (3, -2), sumbu mayor sejajar sumbu y dengan panjang 10, dan sumbu minor dengan panjang 6.
Pembahasan:
Diketahui:
– Pusat elips di (h, k) = (3, -2)
– Panjang sumbu mayor = 2a = 10, maka a = 5
– Panjang sumbu minor = 2b = 6, maka b = 3
– Sumbu mayor sejajar sumbu y
Persamaan elips dengan pusat (h, k) dan sumbu mayor sejajar sumbu y adalah:
$$ \frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1 $$
$$ \frac{(x-3)^2}{9} + \frac{(y+2)^2}{25} = 1 $$
Soal 36
Tentukan koordinat fokus dan panjang latus rectum dari elips $$ \frac{x^2}{36} + \frac{y^2}{20} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{x^2}{36} + \frac{y^2}{20} = 1 $$, diperoleh a² = 36 dan b² = 20.
Maka a = 6 dan b = 2√5.
Untuk mencari nilai c:
c² = a² – b² = 36 – 20 = 16
c = 4
Karena sumbu mayor terletak pada sumbu x (a² > b²), maka koordinat fokus adalah:
F₁(-4, 0) dan F₂(4, 0)
Panjang latus rectum elips adalah $$ \frac{2b^2}{a} $$
$$ \frac{2 \times 20}{6} = \frac{40}{6} = \frac{20}{3} $$
Jadi, koordinat fokus elips adalah (-4, 0) dan (4, 0), sedangkan panjang latus rectumnya adalah 20/3 satuan.
Soal 37
Sebuah elips memiliki persamaan $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ dengan a > b > 0. Jika eksentrisitasnya 1/2 dan salah satu fokusnya adalah (3, 0), tentukan nilai a dan b.
Pembahasan:
Diketahui:
– Eksentrisitas e = 1/2
– Salah satu fokus di (3, 0), maka c = 3
Hubungan eksentrisitas dengan parameter elips: e = c/a
1/2 = 3/a
a = 3 × 2 = 6
Dari nilai c dan a, kita cari nilai b:
c² = a² – b²
3² = 6² – b²
9 = 36 – b²
b² = 36 – 9 = 27
b = 3√3
Jadi, nilai a = 6 dan b = 3√3.
Soal 38
Titik (8, 0) merupakan salah satu ujung sumbu mayor sebuah elips dengan eksentrisitas 3/4. Tentukan persamaan elips tersebut.
Pembahasan:
Diketahui:
– Titik ujung sumbu mayor adalah (8, 0), maka a = 8
– Eksentrisitas e = 3/4
Hubungan eksentrisitas dengan parameter elips: e = c/a
3/4 = c/8
c = 8 × 3/4 = 6
Dari nilai c dan a, kita cari nilai b:
c² = a² – b²
6² = 8² – b²
36 = 64 – b²
b² = 64 – 36 = 28
b = 2√7
Persamaan elips dengan sumbu mayor pada sumbu x adalah:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{64} + \frac{y^2}{28} = 1 $$
Soal 39
Tentukan persamaan garis singgung elips $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$ di titik (0, 3).
Pembahasan:
Dari persamaan $$ \frac{x^2}{16} + \frac{y^2}{9} = 1 $$, diperoleh a² = 16 dan b² = 9.
Maka a = 4 dan b = 3.
Persamaan garis singgung elips $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ di titik (x₀, y₀) adalah:
$$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1 $$
Dengan titik singgung (0, 3), persamaan garis singgungnya adalah:
$$ \frac{0 \times x}{16} + \frac{3 \times y}{9} = 1 $$
$$ \frac{3y}{9} = 1 $$
$$ y = 3 $$
Jadi, persamaan garis singgung elips di titik (0, 3) adalah y = 3.
Soal 40
Tentukan titik-titik potong elips $\frac{(x-1)^2}{9} + \frac{(y+2)^2}{4} = 1$ dengan sumbu-sumbu koordinat.
Pembahasan:
Elips dengan persamaan $\frac{(x-1)^2}{9} + \frac{(y+2)^2}{4} = 1$ memiliki pusat di (1, -2).
Untuk mencari titik potong dengan sumbu-x, substitusi y = 0:
$\frac{(x-1)^2}{9} + \frac{(0+2)^2}{4} = 1$
$\frac{(x-1)^2}{9} + \frac{4}{4} = 1$
$\frac{(x-1)^2}{9} = 1 – 1 = 0$
$(x-1)^2 = 0$
$x = 1$
Jadi, elips berpotongan dengan sumbu x di titik (1, 0).
Untuk mencari titik potong dengan sumbu-y, substitusi x = 0:
$\frac{(0-1)^2}{9} + \frac{(y+2)^2}{4} = 1$
$\frac{1}{9} + \frac{(y+2)^2}{4} = 1$
$\frac{(y+2)^2}{4} = 1 – \frac{1}{9} = \frac{9-1}{9} = \frac{8}{9}$
$(y+2)^2 = \frac{8 \cdot 4}{9} = \frac{32}{9}$
$y+2 = \pm \sqrt{\frac{32}{9}} = \pm \frac{4\sqrt{2}}{3}$
$y = -2 \pm \frac{4\sqrt{2}}{3}$
Jadi, elips berpotongan dengan sumbu y di titik $(0, -2 + \frac{4\sqrt{2}}{3})$ dan $(0, -2 – \frac{4\sqrt{2}}{3})$.
Soal 41
Tentukan persamaan elips yang memiliki fokus di $(±4, 0)$ dengan eksentrisitas 0,5.
Pembahasan:
Diketahui $c = 4$ dan $e = 0,5$. Dari rumus $e = \frac{c}{a}$, kita peroleh $a = \frac{c}{e} = \frac{4}{0,5} = 8$.
Kemudian, $b^2 = a^2 – c^2 = 64 – 16 = 48$, sehingga $b = 4\sqrt{3}$.
Persamaan elipsnya: $$ \frac{x^2}{64} + \frac{y^2}{48} = 1 $$
Soal 42
Tentukan luas daerah yang dibatasi oleh elips $16x^2 + 9y^2 = 144$.
Pembahasan:
Ubah persamaan menjadi $$ \frac{x^2}{9} + \frac{y^2}{16} = 1 $$.
Maka $a = 3$ dan $b = 4$.
Luas elips $= \pi ab = 12\pi$ satuan luas.
Soal 43
Tentukan persamaan elips dengan panjang sumbu mayor $10$, panjang sumbu minor $6$, dan pusat di titik $(2, -3)$.
Pembahasan:
Diketahui $2a = 10$ dan $2b = 6$, maka $a = 5$ dan $b = 3$.
Dengan pusat di $(h,k) = (2,-3)$, persamaan elipsnya adalah $$ \frac{(x-2)^2}{25} + \frac{(y+3)^2}{9} = 1 $$
Soal 44
Tentukan koordinat fokus dari elips $9x^2 + 4y^2 – 18x + 16y + 1 = 0$.
Pembahasan:
Langkah 1: Ubah ke bentuk standar.
$9(x^2 – 2x) + 4(y^2 + 4y) + 1 = 0$
$9(x^2 – 2x + 1 – 1) + 4(y^2 + 4y + 4 – 4) + 1 = 0$
$9(x – 1)^2 – 9 + 4(y + 2)^2 – 16 + 1 = 0$
$9(x – 1)^2 + 4(y + 2)^2 = 24$
$$ \frac{(x-1)^2}{8/3} + \frac{(y+2)^2}{6} = 1 $$
Pusat di $(1, -2)$, $a = \sqrt{\frac{8}{3}}$ dan $b = \sqrt{6}$. Karena $b > a$, sumbu mayor pada sumbu $y$.
$c^2 = b^2 – a^2 = 6 – \frac{8}{3} = \frac{10}{3}$, sehingga $c = \sqrt{\frac{10}{3}}$.
Fokus di $(1, -2\pm\sqrt{\frac{10}{3}}) = (1, -2+\sqrt{\frac{10}{3}})$ dan $(1, -2-\sqrt{\frac{10}{3}})$.
Soal 45
Tentukan persamaan parametrik elips $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$.
Pembahasan:
Untuk elips $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$, persamaan parametriknya adalah $x = a\cdot\cos(t)$ dan $y = b\cdot\sin(t)$.
Dengan $a = 5$ dan $b = 3$, maka persamaan parametriknya adalah $x = 5\cos(t)$ dan $y = 3\sin(t)$, dengan $0 \leq t < 2\pi$.
Soal 46
Sebuah elips memiliki fokus di $(0, \pm4)$ dan eksentrisitas $e = 0,8$. Tentukan persamaan elips tersebut.
Pembahasan:
Dengan fokus di $(0, \pm4)$, maka $c = 4$ dan sumbu mayor pada sumbu $y$.
Dari $e = \frac{c}{a}$, kita peroleh $a = \frac{c}{e} = \frac{4}{0,8} = 5$.
Kemudian $b^2 = a^2 – c^2 = 25 – 16 = 9$, sehingga $b = 3$.
Persamaan elipsnya adalah $$ \frac{x^2}{9} + \frac{y^2}{25} = 1 $$
Soal 47
Tentukan persamaan elips jika diketahui titik puncaknya adalah $(0, \pm3)$ dan fokusnya di $(0, \pm2)$.
Pembahasan:
Dari titik puncak $(0, \pm3)$, kita peroleh $a = 3$ dan sumbu mayor pada sumbu $y$.
Dari fokus $(0, \pm2)$, kita peroleh $c = 2$.
$b^2 = a^2 – c^2 = 9 – 4 = 5$, sehingga $b = \sqrt{5}$.
Persamaan elipsnya adalah $$ \frac{x^2}{5} + \frac{y^2}{9} = 1 $$
Soal 48
Tentukan persamaan elips yang berpusat di origin, dengan sumbu mayor pada sumbu $x$, panjang sumbu mayor $10$, dan panjang latus rectum $6$.
Pembahasan:
Diketahui $2a = 10$, maka $a = 5$.
Panjang latus rectum $= \frac{2b^2}{a} = 6$
$\frac{2b^2}{5} = 6$
$b^2 = 15$
$b = \sqrt{15}$
Persamaan elipsnya adalah $$ \frac{x^2}{25} + \frac{y^2}{15} = 1 $$
Soal 49
Tentukan jenis dan persamaan kurva yang memenuhi persamaan $4x^2 + 9y^2 + 16x – 18y – 11 = 0$.
Pembahasan:
Langkah 1: Kelompokkan suku-suku.
$4(x^2 + 4x) + 9(y^2 – 2y) – 11 = 0$
$4(x^2 + 4x + 4 – 4) + 9(y^2 – 2y + 1 – 1) – 11 = 0$
$4(x + 2)^2 – 16 + 9(y – 1)^2 – 9 – 11 = 0$
$4(x + 2)^2 + 9(y – 1)^2 = 36$
$$ \frac{(x+2)^2}{9} + \frac{(y-1)^2}{4} = 1 $$
Ini adalah persamaan elips dengan pusat di $(-2, 1)$, $a = 3$, dan $b = 2$.
Soal 50
Tentukan persamaan garis singgung elips $$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$ yang melalui titik $(8, 6)$.
Pembahasan:
Persamaan garis singgung elips $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ dari titik luar $(x_1, y_1)$ dapat ditulis sebagai $$\frac{xx_1}{a^2} + \frac{yy_1}{b^2} = 1 + \frac{x_1^2-a^2}{a^2} + \frac{y_1^2-b^2}{b^2}$$.
Dengan $a = 5$, $b = 4$, $x_1 = 8$, $y_1 = 6$, kita substitusi:
$$\frac{8x}{25} + \frac{6y}{16} = 1 + \frac{64-25}{25} + \frac{36-16}{16}$$
$$\frac{8x}{25} + \frac{6y}{16} = 1 + \frac{39}{25} + \frac{20}{16}$$
$$\frac{8x}{25} + \frac{6y}{16} = 1 + 1.56 + 1.25 = 3.81$$
$$\frac{8x}{25} + \frac{6y}{16} = 3.81$$
Ini adalah persamaan garis singgung yang melalui titik $(8, 6)$.
Soal 51
Tentukan persamaan elips jika titik $(4, 3)$ terletak pada elips, fokusnya di $(\pm3, 0)$, dan sumbu mayornya pada sumbu $x$.
Pembahasan:
Dengan fokus di $(\pm3, 0)$, maka $c = 3$ dan sumbu mayor pada sumbu $x$.
Misalkan persamaan elips adalah $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ dengan $a$ dan $b$ belum diketahui.
Karena titik $(4, 3)$ terletak pada elips, maka $$ \frac{4^2}{a^2} + \frac{3^2}{b^2} = 1 $$.
Kita juga tahu bahwa $c^2 = a^2 – b^2$, dengan $c = 3$.
$9 = a^2 – b^2$
$b^2 = a^2 – 9$
Substitusi ke persamaan pertama: $$ \frac{16}{a^2} + \frac{9}{a^2-9} = 1 $$
Dengan menyelesaikan persamaan, diperoleh $a = 5$ dan $b = 4$.
Persamaan elipsnya adalah $$ \frac{x^2}{25} + \frac{y^2}{16} = 1 $$
Soal 52
Tentukan persamaan elips dengan pusat di origin dan sumbu mayor pada sumbu $x$ jika diketahui persamaan direktrisnya adalah $x = \pm5$.
Pembahasan:
Persamaan direktris elips adalah $x = \pm\frac{a}{e}$, dengan $a =$ panjang setengah sumbu mayor dan $e =$ eksentrisitas.
Dari soal, $\frac{a}{e} = 5$.
Elips memiliki persamaan $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$.
Kita tahu $e = \frac{c}{a}$ dan $c^2 = a^2 – b^2$.
$\frac{a}{e} = 5$ berarti $a = 5e$. Substitusi ke $e = \frac{c}{a}$:
$e = \frac{c}{5e}$
$e^2 = \frac{c}{5}$
$5e^2 = c$
Kemudian $c^2 = a^2 – b^2 = (5e)^2 – b^2 = 25e^2 – b^2$
Ini berarti $(5e^2)^2 = 25e^4 = 25e^2$
Untuk memenuhi ini, kita bisa mengambil $e = \frac{4}{5}$, sehingga $a = 5e = 5 \times \frac{4}{5} = 4$ dan $c = 5e^2 = 5 \times \frac{16}{25} = \frac{16}{5}$.
Kemudian $b^2 = a^2 – c^2 = 16 – \frac{256}{25} = \frac{400}{25} – \frac{256}{25} = \frac{144}{25}$, sehingga $b = \frac{12}{5}$.
Persamaan elipsnya adalah $$ \frac{x^2}{16} + \frac{y^2}{144/25} = 1 $$ atau $$ \frac{25x^2}{400} + \frac{25y^2}{144} = 1 $$
Soal 53
Tentukan persamaan garis yang menyinggung elips $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$ dan sejajar dengan garis $2x + y – 4 = 0$.
Pembahasan:
Garis $2x + y – 4 = 0$ dapat ditulis sebagai $y = -2x + 4$, dengan gradien $m = -2$.
Garis singgung yang dicari memiliki persamaan $y = -2x + k$ untuk suatu konstanta $k$.
Substitusi ke persamaan elips: $$ \frac{x^2}{9} + \frac{(-2x+k)^2}{4} = 1 $$
$$ \frac{4x^2}{36} + \frac{4x^2-4kx+k^2}{4} = 1 $$
$$ \frac{x^2}{9} + x^2 – kx + \frac{k^2}{4} = 1 $$
$$ \frac{x^2}{9} + x^2 – kx + \frac{k^2}{4} – 1 = 0 $$
Untuk menjadi garis singgung, persamaan ini harus memiliki diskriminan $= 0$.
Dengan menyelesaikan, kita akan mendapatkan $k = \pm5$.
Jadi, persamaan garis singgungnya adalah $y = -2x + 5$ atau $y = -2x – 5$.
Soal 54
Sebuah elips memiliki fokus di $(\pm6, 0)$ dan salah satu titik ujung sumbu minornya adalah $(0, 4)$. Tentukan persamaan elips tersebut.
Pembahasan:
Dengan fokus di $(\pm6, 0)$, maka $c = 6$ dan sumbu mayor pada sumbu $x$.
Dari titik ujung sumbu minor $(0, 4)$, maka $b = 4$.
Kita cari nilai $a$: $c^2 = a^2 – b^2$
$6^2 = a^2 – 4^2$
$36 = a^2 – 16$
$a^2 = 52$
$a = 2\sqrt{13}$
Persamaan elipsnya adalah $$ \frac{x^2}{52} + \frac{y^2}{16} = 1 $$
Soal 55
Tentukan eksentrisitas elips yang memiliki persamaan $25x^2 + 16y^2 = 400$.
Pembahasan:
Ubah persamaan menjadi $$ \frac{x^2}{16} + \frac{y^2}{25} = 1 $$.
$a = 5$ dan $b = 4$, dengan sumbu mayor pada sumbu $y$.
$c^2 = a^2 – b^2 = 25 – 16 = 9$, sehingga $c = 3$.
Eksentrisitas $e = \frac{c}{a} = \frac{3}{5} = 0,6$.
Soal 56
Tentukan persamaan elips yang memiliki eksentrisitas $e = 0,8$ dan titik ujung sumbu minornya adalah $(0, \pm3)$.
Pembahasan:
Dari titik ujung sumbu minor $(0, \pm3)$, kita peroleh $b = 3$ dan sumbu mayor pada sumbu $x$.
Dari $e = \frac{c}{a}$ dan $c^2 = a^2 – b^2$:
$e^2 = \frac{c^2}{a^2} = \frac{a^2 – b^2}{a^2} = 1 – \frac{b^2}{a^2}$
$0,8^2 = 1 – \frac{9}{a^2}$
$0,64 = 1 – \frac{9}{a^2}$
$\frac{9}{a^2} = 0,36$
$a^2 = \frac{9}{0,36} = 25$
$a = 5$
Persamaan elipsnya adalah $$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Soal 57
Tentukan persamaan elips jika fokusnya di $(\pm2, 0)$ dan jarak antara kedua direktrisnya adalah $20$.
Pembahasan:
Dengan fokus di $(\pm2, 0)$, maka $c = 2$ dan sumbu mayor pada sumbu $x$.
Jarak antara kedua direktris $= \frac{2a}{e} = 20$
$\frac{a}{e} = 10$
Kita juga tahu $e = \frac{c}{a}$, sehingga:
$\frac{c}{a} = e = \frac{a}{10}$
$\frac{2}{a} = \frac{a}{10}$
$2 \times 10 = a^2$
$a^2 = 20$
$a = 2\sqrt{5}$
Kemudian $c^2 = a^2 – b^2$
$4 = 20 – b^2$
$b^2 = 16$
$b = 4$
Persamaan elipsnya adalah $$ \frac{x^2}{20} + \frac{y^2}{16} = 1 $$
Soal 58
Tentukan koordinat fokus dan eksentrisitas elips $$ \frac{(x-1)^2}{25} + \frac{(y+2)^2}{16} = 1 $$.
Pembahasan:
Dari persamaan $$ \frac{(x-1)^2}{25} + \frac{(y+2)^2}{16} = 1 $$, kita peroleh:
Pusat di $(h, k) = (1, -2)$
$a = 5$ dan $b = 4$
$c^2 = a^2 – b^2 = 25 – 16 = 9$, sehingga $c = 3$
Karena sumbu mayor sejajar sumbu $x$, fokus terletak di $(1\pm3, -2) = (4, -2)$ dan $(-2, -2)$.
Eksentrisitas $e = \frac{c}{a} = \frac{3}{5} = 0,6$.
Soal 59
Titik $(5, 0)$ adalah salah satu titik ujung sumbu mayor sebuah elips. Jika perbandingan panjang sumbu mayor dan sumbu minor adalah $3:2$, tentukan persamaan elips tersebut.
Pembahasan:
Dari titik ujung sumbu mayor $(5, 0)$, kita peroleh $a = 5$ dan sumbu mayor pada sumbu $x$.
Jika perbandingan $a:b = 3:2$, maka $b = \frac{2a}{3} = \frac{2\times5}{3} = \frac{10}{3}$.
Persamaan elipsnya adalah $$ \frac{x^2}{25} + \frac{y^2}{100/9} = 1 $$ atau $$ \frac{9x^2}{225} + \frac{9y^2}{100} = 1 $$
Soal 60
Tentukan luas daerah yang dibatasi oleh elips dengan persamaan $4x^2 + 9y^2 – 8x + 36y + 4 = 0$.
Pembahasan:
Langkah 1: Ubah ke bentuk standar.
$4(x^2 – 2x) + 9(y^2 + 4y) + 4 = 0$
$4(x^2 – 2x + 1 – 1) + 9(y^2 + 4y + 4 – 4) + 4 = 0$
$4(x – 1)^2 – 4 + 9(y + 2)^2 – 36 + 4 = 0$
$4(x – 1)^2 + 9(y + 2)^2 = 36$
$$ \frac{(x-1)^2}{9} + \frac{(y+2)^2}{4} = 1 $$
Ini adalah persamaan elips dengan pusat di $(1, -2)$, $a = 3$, dan $b = 2$.
Luas elips $= \pi ab = \pi \times 3 \times 2 = 6\pi$ satuan luas.